В моей последней статье мы рассмотрели несколько относительно простых, но фундаментальных определений, лежащих в основе биомеханики спорта и упражнений, и связали их с махами гирями.
Теперь, хотя это и очень интересно, мы не особо вдавались в подробности, а детали могут быть важны, особенно когда мы говорим о том, как мы применяем силы, вызывающие движение.
В моей последней статье мы рассмотрели несколько относительно простых, но фундаментальных определений, лежащих в основе биомеханики спорта и упражнений, и связали их с махами гирями
Теперь, хотя это и очень интересно, мы не особо вдавались в подробности, а детали могут быть важны, особенно когда мы говорим о том, как мы применяем силы, вызывающие движение.
Эта статья будет посвящена важному типу модели движения: кривым сила-время, которые иллюстрируют, как мы применяем силу во времени
Мы объединим это с объяснением законов движения Ньютона и того, как они соотносятся с изучением спорта и упражнений с использованием вертикального прыжка в противодействии (в котором испытуемый сгибается в бедрах и коленях перед прыжком). Понимание этого создает основу для будущих обзоров.
Резюме: Что такое Сила?
Вспомните, что «сила - это толкающее или тянущее действие, которое один объект оказывает на другой». Итак, если мы хотим что-то сдвинуть, будь то штанга, гиря или собственное тело, мы должны это толкнуть или потянуть - применить силу.
В случае с нашим прыгуном сила прикладывается к его центру масс, точке, вокруг которой распределяются массы его сегментов (например, рук и ног), чтобы помочь сохранить равновесие.
Три закона Ньютона о линейном движении обеспечивают основу того, как мы управляем движением с помощью силы, и влияние, которое это может иметь на производительность. Приложение силы для движения будет работать только в том случае, если оно достаточно для преодоления инерции объекта - первый закон Ньютона: закон инерции.
Инерция: он не двигается сам
Инерция - одно из тех слов, которыми обычно злоупотребляют. По отношению к первому закону Ньютона инерция - это нежелание объекта изменять свое состояние, где состояние просто указывает на то, движется он или нет. Именно это состояние контролируется приложением силы.
Итак, объект будет оставаться неподвижным до тех пор, пока его не толкнут или не потянут - приложена сила. Или, однажды двигаясь, он будет продолжать двигаться; пока не толкнули или не потянули, то есть, как вы уже догадались, приложив силу
Но как мы можем управлять этим состоянием? Раздача - это стандартная единица, в которой сообщается инерция: килограмм, единица, также используемая для сообщения массы (ну, во всяком случае, в большинстве стран мира).
Это вводит, пожалуй, самый основной тип силы: вес, который является произведением массы и ускорения свободного падения. Следовательно, чтобы преодолеть инерцию (сдвинуть что-либо) объекта, мы должны приложить силу, превышающую его вес.
Кривые сила-время: базовая схема движения человека
С практической точки зрения это может стать весьма захватывающим. Движение человека, как правило, опирается на приложение силы к земле ногами (или руками, см. статью Бекки о силе отжиманий).
Платформы Force позволяют нам регистрировать эти силы, и, используя законы Ньютона, мы можем манипулировать ими, чтобы лучше понять механические требования различных типов движения (см., например, предыдущую статью).
И тем не менее, чтобы вернуться к прежнему курсу, на Рисунке 1 показана типичная кривая вертикальной силы-времени, полученная в результате выполнения вертикального прыжка.
Рисунок 1. Типичная кривая зависимости вертикальной силы от времени при выполнении вертикального прыжка в обратном направлении, вертикальная сила приложена к центру масс нашего прыгуна.
Одним из первых действий, которые мы обычно делаем, чтобы понять кривую сила-время, является определение веса субъекта в период «спокойного стояния», который можно увидеть на рисунке 2
В данном случае масса тела составляет 787 ньютонов; деление этого на ускорение свободного падения (9,81) дает массу тела чуть более 80 кг. Затем мы можем начать думать о применении второго закона Ньютона, чтобы получить больше информации о том, какая сила была приложена и какое движение это вызовет.
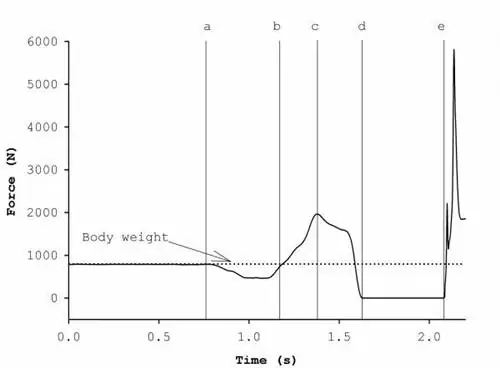
Рисунок 2. Аннотированная вертикальная кривая сила-время.
- Ось «у» до точки «а» показывает «спокойное стояние», которое равно массе тела испытуемого
- Точки от «а» до «b» показывают «разгрузку» - субъект опускает колени, двигаясь в том же направлении, что и ускорение силы тяжести
- Точки от «b» до «c» показывают увеличение силы до пика, когда субъект замедляет движение вниз до нижней точки провала
- Точки с ‘c’ по ‘d’ показывают «активную» силу прыжка (разгибание ноги)
- Точка «d» показывает «взлет»; точки от «d» до «e» «полетное» или «воздушное» время
Сила, масса и ускорение
Вспомним из прошлой статьи, что сила есть произведение массы на ускорение (F=ma), и мы можем использовать это для расшифровки рисунков 1 и 2
Если мы знаем, что F=ma, мы можем манипулировать данными о силе, как показано на рисунках 1 и 2, путем деления их на массу объекта, преобразуя нашу кривую сила-время в кривую ускорение-время..
Однако нам нужно помнить о первом законе Ньютона, где мы должны преодолеть вес нашего прыгуна: 787 ньютонов. Мы можем просто вычесть вес тела из рисунка 1, прежде чем разделить его на массу, что сделает силу «спокойного стояния» равной нулю.
Сила должна быть больше нуля, чтобы влиять на движение или ускорять массу нашего прыгуна. Пример нашей кривой зависимости ускорения от времени можно увидеть на рисунке 3.
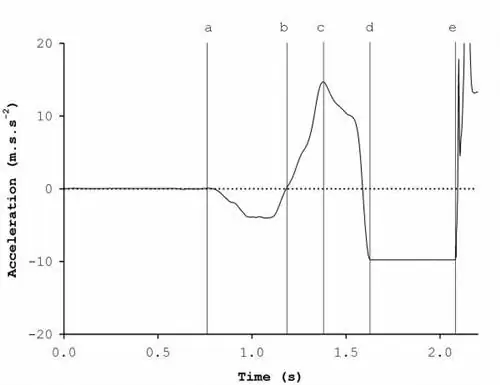
Рисунок 3. Аннотированная кривая зависимости вертикального ускорения от времени - ускорение центра масс нашего прыгуна во время его прыжка.
Это здорово, но ничего нам не говорит. Однако небольшая махинация в виде численного интегрирования позволяет рассчитать скорость - насколько быстро движется наш прыгун.
Рисунок 4 показывает скорость-время, а также то, что часто называют пиками и впадинами, которые указывают направление движения: впадины ниже нуля указывают на нисходящее движение, пики выше нуля - восходящее движение.
Мы могли бы пойти дальше и численно интегрировать эти данные о скорости и времени, чтобы получить смещение или движение, но ключевые параметры, такие как высота прыжка, могут быть довольно легко получены с использованием уравнений равномерного движения.
Для этого нам нужно определить скорость нашего парашютиста при взлете, возвести ее в квадрат, а затем разделить на 2 g (9,812), что в данном случае равно следующему:
5,34 (2,31 [взлетная скорость2]) ÷19,62 (2 г)=27 (см) (довольно посредственно)
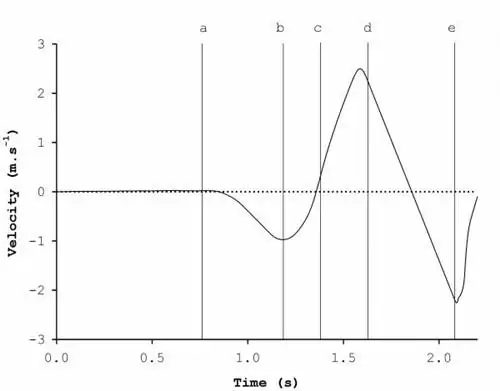
Рисунок 4. Аннотированная вертикальная кривая скорость-время - насколько быстро перемещается центр масс нашего прыгуна во время его прыжка.
Сейчас мы вычисляем механическую мощность, умножая наши данные сила-время на наши блестящие новые данные скорость-время, но давайте оставим это для другой статьи, где мы сможем отдать должное теме.
Прежде чем мы закончим, мы должны рассмотреть практическую значимость третьего закона Ньютона
Действие: Реакция
Это, пожалуй, самый известный закон Ньютона, и он гласит, что на каждое действие есть равное и противоположное противодействие
Возможно, не осознавая этого, этот закон действовал на протяжении всего нашего анализа, поскольку, если бы наш прыгун оттолкнулся от земли и не встретил равной противоположной реакции, выполнение прыжка было бы довольно сложным.
Видите ли, именно эта реакция - в сочетании со вторым законом Ньютона (и трением) - позволяет нам контролировать то, как мы двигаемся, и ее становится намного легче понять, когда мы понимаем законы 1 и 2.
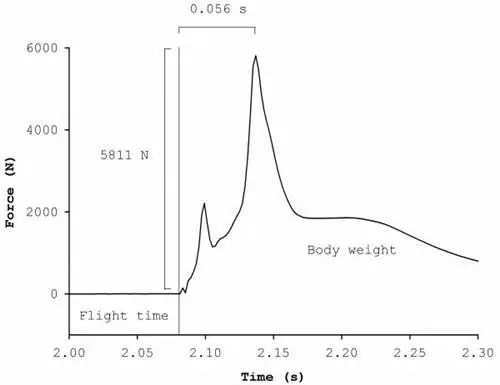
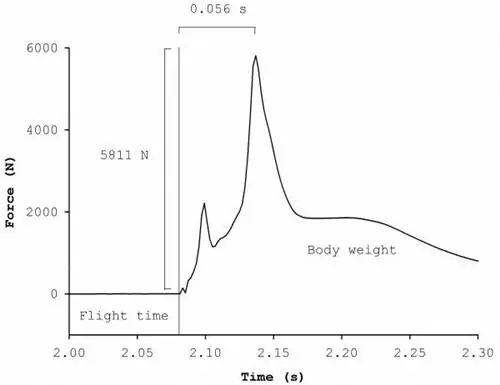
Рисунок 5. Силы при вертикальном прыжковом приземлении.
Единственным недостатком этого является то, что это также приводит к механическим последствиям. Хотя реакция позволяет нам двигаться, она также может действовать как важнейшая тормозная сила, приводящая движение к падению. стоп.
Это показано на рис. 5, где основное внимание уделяется изменению вертикальной силы при приземлении нашего прыгуна. Действительно, до этого момента наш анализ был сосредоточен на первой цели биомеханики: улучшить производительность, в то время как силы, показанные на рисунке 5, позволяют нам учитывать вторую цель биомеханики: минимизировать травму.
Выявление проблемных зон, таких как приземление в прыжке, позволяет нам вносить изменения в технику стратегии приземления с целью уменьшения силы приземления и, таким образом, минимизации травм
Наш парашютист остановился с помощью силы, почти в 7,5 раз превышающей вес его тела. И наконец, рисунок 5 также может показать нам, как быстро к телу была приложена посадочная сила. В данном случае это было 56 миллисекунд (0,056 секунды).
Деление посадочной силы на время приземления дает нечто, называемое скоростью загрузки, которая в данном случае составляла чуть менее132 единиц массы тела в секунду - потенциально проблематично.
В заключение, мы можем использовать закон движения Ньютона, чтобы манипулировать данными сила-время, чтобы получить представление о различных фазах производительности, таких как вертикальный прыжок, его требования и последствия.